Jak na TSP - Symbolické myšlení - Hledání spojitosti

1. Hledat v čem spočívá problematika příkladu

Příklady této kapitoly jsou opravdu velmi zrádné, a často bývá užitečné takový příklad mezi ostatními co nejdříve rozpoznat a případně jej rovnou přeskočit - a to pokud usoudíme, že jeho řešení se může protáhnout na dlouhou chvíli a že rychlost jeho vyřešení v jistém smyslu spočívá na náhodě.

Pokud se přesto pokusíme příklad vyřešit, nejužitečnější praktikou je neustálé hledání souvislostí v příkladu (pořád něco zkoušet, porovnávat, počítat...).

Ukažme si to na příkladě:

Jelikož byl příklad součástí symbolického myšlení, někoho by mohlo napadnout - pohlížet na jednotlivé číslice jako na symboly (vizte podstatu ukázkového příkladu v prvním videu). Takové myšlenky však vedou na scestí a člověk takto pouze nevědomky ztrácí nějaký čas...

Po chvilce neúspěšného hledání se tedy pokusí na čísla pohlížet jako na časové údaje (přece jen se jedná o digitální hodiny) - například porovnávat rozdíly mezi jednotlivými časovými údaji apod. Tento přístup však také nevede ke správnému výsledku a my tak ztratíme další čas neúspěšnými výpočty.

Počítat ciferný součet nás může napadnout například až nyní (případně ještě později) - pak zjistíme, že ciferné součty jednotlivých hodin jsou postupně 15-6-15-6-? a že tedy ciferný součet posledních hodin bude nejspíš opět 15.

Tímto chci ukázat, že do jisté míry záleží na náhodě, kdy se vaše myšlenky začnou ubírat správným směrem. Je také možné že řešení s ciferným součtem vás napadne ihned a příklad tedy máte hotový během chvilky.

Jak jsem říkal, mým hlavním doporučením je tedy rychle se pokusit nalézt správné spojitosti, pokud však nad příkladem budete trávit již podezřele dlouhý čas, bude lepší jej přeskočit.

2. Vyřešit příklad

Po nalezení správné spojitosti v příkladu už většinou není problém určit správný výsledek - v našem případě hledáme z nabízených hodin ty, které mají ciferný součet 15 (možnost D).

Další příklady pro zajímavost:

Pro zajímavost zde umístím ukázku dalších dvou klasických příkladů této skupiny - nad jejich podstatou jsem já například trávil několik hodin, přestože jsem věděl, jaký je správný výsledek - tedy klasičtí představitelé příkladů na přeskočení po krátké snaze o vyřešení.

Podstatu prvního z nich pro zajímavost vizte v prvním ukázkovém videu.

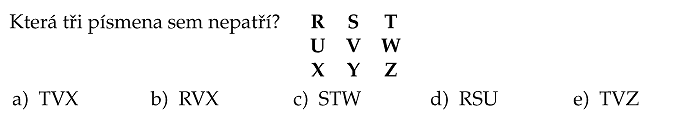
Zadání druhého zní:

Zadání radí, že větve, jablka a kořeny šlechtěných stromů jsou ve vzájemném vztahu. Bude tedy určitě užitečné si napsat jednotlivé počty těchto částí. Zadání však stále nechává ve vzduchu velké množství nejasností - a to je právě to, co příklad opět dělá velmi záludným. Například dopředu nevíme, zdali hrají nějakou roli počty větví nalevo/napravo od kmenů, nebo třeba nahodilé umístění jablek na větvích apod. Proto se opět nabízí spousta směrů, kudy se naše myšlenky mohou vydat.

Tentokrát přeskočíme scestné myšlenky a uchýlíme se rovnou ke správnému směru - tedy že existuje univerzální rovnice, do které když do proměnných dosadíme celkový počet větví, celkový počet jablek a celkový počet kořenů, vyjde nám pro šlechtěné stromy vždy stejný výsledek, kdežto u nešlechtěných výsledek jiný.

Podstatou tohoto příkladu tedy je, že trojnásobek počtu větví šlechtěného stromu se rovná součtu počtu kořenů a dvojnásobku počtu jablek. Tedy rovnice 3v = k + 2j.

• A: 3x6 = 18; 10 + 2x4 = 18
• B: 3x4 = 12; 10 + 2x1 = 12
• C: 3x4 = 12; 6 + 2x2 = 10
• D: 3x5 = 15; 9 + 2x3 = 15
• E: 3x6 = 18; 8 + 2x5 = 18
• F: 3x5 = 15; 10 + 2x2 = 14

 Vidíme tedy, že kromě stromu F nám počty nesedí také u stromu C.