Uspořádání

Teorie

1. Sestavení stromu (schématu) uspořádání

Velice užitečnou pomůckou při řešení těchto příkladů je nákres stromu uspořádání. Ukažme si tedy, jak se strom uspořádání vytváří, a také, jak se s ním pracuje, jelikož to nemusí být zcela intuitivní.

Nejdříve odlišný pohled na situaci - pro lepší pochopení:

Máme tedy pětici přítelkyň s různým věkem a zajímá nás jejich celkové uspořádání. Už na základě první věty si můžeme uvědomit, že lze situaci popsat výčtem všech konkrétních možností, jak mohou být tyto přítelkyně uspořádány od nejstarší po nejmladší. Takových možností, jak je vzájemně uspořádat je právě n!... (permutace n prvků do n pozic). Jelikož umisťujeme 5 přítelkyň - možných uspořádání je 5! tedy 120.

Další věty nám situaci blíže popisují - jedná se tedy o jistá omezení situace:

A je starší než C (A>C)
B je starší než A (B>A)
D je starší než E (D>E)
E je starší než C (E>C)

Každé porovnání dvojic nám z těchto 120ti možností eliminuje jisté možnosti - například, porovnání A>C nám eliminuje ty možnosti, kde C>=A (jelikož má každá z přítelkyň různý věk, stačí psát C>A). Pokud si vyškrtáme možnosti odporující všem výše zmíněným odrážkám, zůstanou nám pouze ty, odpovídají našemu zadání.

Pozn. Tento pohled na příklady je také popsán v druhé části 5. videa - od 8:06.

Nyní už k sestavování stromu:

Výše zmíněný postup je příliš zdlouhavý a těžkopádný, vzhledem k velkému množství možností, ze kterých vycházíme. Eliminovat nevyhovující možnosti lze naštěstí i rychlejším způsobem - právě pomocí sestavení stromu uspořádání.

Načrtneme si, jak lze postupovat na základě informací z odrážek:

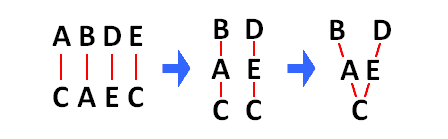
První část obrázku je prostý přepis odrážek - každou dvojici spojíme čarou tak, aby "lepší" prvek byl nad "horším".

Druhá část obrázku využívá násobného výskytu některých prvků z předešlé části. Vytvoří se nám tak delší řetězce. Zde je vhodné si uvědomit princip tranzitivity: tedy je-li např. B>A a zároveň A>C, pak pochopitelně B>C.

Třetí část obrázku je již konečný strom uspořádání - jednotlivé části jsou spojeny do jediného stromu, kde se každý prvek vyskytuje pouze jednou.

Pozn. Sestavování stromů se věnují všechny videa této kapitoly.

2. Čtení informací ze stromu uspořádání

Abyste se stromem mohli správně pracovat (neudělat chybu při jeho čtení), je třeba mít na paměti určitá pravidla.

Pokud například v našem případě z prvku C vystupují dvě větve, je třeba si uvědomit, že tyto větve jsou na sobě nezávislé - tedy nelze je vzájemně porovnat, a tedy je potřeba počítat se všemi možnostmi jejich vzájemného uspořádání. Například z pohledu prvku A víme, že B>A>C, ale nejsme schopni s jistotou říct, zda A>D>E nebo D>A>E nebo D>E>A. Při všech těchto pozicích prvku A je navíc třeba ještě uvažovat několik pozic prvku B, jelikož se vůči pozicím zbývajících prvků může také lišit.

Velmi užitečná může být tato názorná pomůcka:

Jednotlivá spojení mezi prvky (písmeny) lze chápat jako gumičky, které lze natahovat do jakýchkoliv délek, různými směry - její konce se však nesmí obrátit vzhůru nohama.

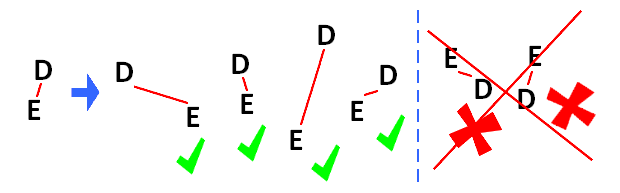
Díky tomuto principu si můžete strom vizuálně transformovat, a představovat si jaká mohou být jednotlivá uspořádání (tento princip je názorně ukázán na posledním obrázku této stránky - jednotlivá uspořádání lze číst po řádcích odshora dolů).

Při určování správného výsledku nám pro jednotlivé odpovědi stačí nalézt pouze jeden protipříklad, pomocí kterého špatné odpovědi eliminujeme a zůstane nám tedy jen ta jediná, která je správnou odpovědí.

Chcete-li přesto sestavit ze stromu všechna možná uspořádání (delší způsob řešení):

Zvolíme si co nejdelší posloupnost, která pouze stoupá (nebo pouze klesá). V našem případě máme 2 možnosti na výběr (posloupnost B>A>C nebo D>E>C), zvolme tedy B-A-C.

Zbývající 2 prvky (D a E) do zvolené posloupnosti nakombinujeme tak, abychom neporušili žádné z pravidel. Takto získáme všechna možná konkrétní uspořádání pětic, která odpovídají našemu zadání.

Začneme tím, že si prvky D a E umístíme co nejníže - jelikož víme, že E>C a že D>E, pak nejnižší možné umístění těchto prvků je to, které znázorňuje 1. posloupnost na následujícím obrázku.

Pro nejnižší umístění prvku D zjistíme všechna možná umístění prvku E (začneme odspodu a postupně jej posouváme nahoru"). Jakmile pro nejnižší pozici prvku D vyčerpáme všechny pozice prvku E (pouze 1. posloupnost na obrázku). Posuneme si prvek D o kousek víš a opět zjišťujeme všechny možné pozice prvku E (2. a 3. posloupnost na obrázku). Takto postupujeme až do situace, kdy prvky D i E "probublají" až na svoje nejvyšší možné pozice (přidána 4., 5. a 6. posloupnost na obrázku) - v ten moment již máme sestavena všechna možná uspořádání.

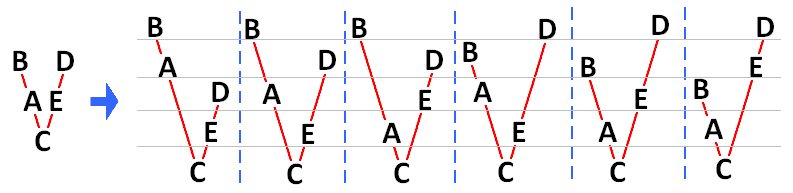
Pozn. Sestavování všech možných uspořádání je podrobně popsáno také v 5. videu - od 2:04.

3. Určení správné odpovědi

Přestože k určení správného výsledku postačí nákres samotného stromu uspořádání, ukázali jsme si další způsob, jak lze zadání reprezentovat (výčet možností, které mohou na základě zadání nastat). Jelikož, žádné z výsledných uspořádání není v rozporu se zadáním, je opravdu potřeba počítat se všemi. Pokud nás tedy zadání vyzývá "Vyberte tvrzení, jehož pravdivost vyplývá z uvedených informací", je potřeba vybrat takové tvrzení, které je pravdivé při všech těchto uspořádáních (s žádným z nich si neodporuje). V našem případě je to tedy pouze tvrzení "Druhá nejmladší je A nebo E".

Číst více