Úseky

Teorie

1. Nakreslit popsanou situaci - na úsečku

Nejlépe si postup ukážeme opět na příkladu:

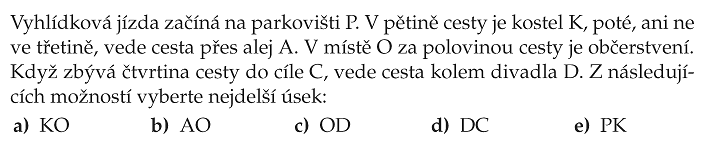
Základem tedy je nakreslit si úsečku s krajními body startovní pozice a cílové pozice:

Kromě krajních bodů je nám popsána i pozice ostatních bodů. U některých bodů je tato pozice pouze přibližná (popisuje mezi kterými body se daný bod nachází) - jelikož tedy zadání nepopisuje přesně, kde se daný bod nachází - je potřeba uvažovat, že bod se může nacházet v celém úseku mezi ohraničeného krajními body.

K - leží přesně v pětině celkové délky úsečky
A - leží někde v úseku mezi první pětinou úsečky a první třetinou úsečky
O - leží někde v úseku mezi polovinou a poslední čtvrtinou úsečky
D - leží přesně na začátku poslední čtvrtiny úsečky (tj. ve 3/4 celkové délky úsečky)

Pozn. Jednotlivé zlomky budeme vždy chápat jako poměr vzhledem k celkové délce trati/úsečky.

Polohu těchto bodů lze znázornit například takto (červeně jsou označeny polohy hraničních bodů vzhledem celkové velikosti úsečky, zeleně jsou vyjádřeny délky úseků - vzdálenosti hraničních bodů):

Pokud se špatně orientujete ve zlomcích (například si hned neuvědomíte, že např. 1/3 > 1/4), je vhodné si například převést všechny zlomky na společného jmenovatele. V příkladu nám vystupují zlomky 1/5; 1/4; 1/3; 1/2 - nejmenší společný násobek jmenovatelů je 60, můžeme je tedy převést do tvaru se stejným jmenovatelem: 12/60; 15/60; 20/60 a 30/60. Takto lze na první pohled zlomky porovnávat (pomocí čitatelů) - jednoznačně 20/60 > 15/60.

Pokud si těžko vybavujete jednotlivé vzdálenosti hraničních bodů - můžete si je do schématu také zapsat, jelikož je to velice užitečné (znázorněny zeleně):

Nyní se obrázek může jevit trošku zmateně... rozhodně vás nenabádám, abyste si vždy takto důsledně vše vypisovali - většinou pro odhalení správného výsledku stačí mnohem méně výpisků. Obrázek slouží spíše jako demonstrativní ukázka, jak se se zlomky pracuje - než budete pokračovat dál, ujistěte se, že všemu dobře rozumíte.

2. Přečíst jednotlicé vzdálenosti úseček

Jak jsem říkal, není třeba si psát veškeré údaje do schématu - důležité však je, abyste všemu ve schématu dokonale rozuměli - pak totiž není většinou problém dojít ke správnému výsledku, pokud budeme šikovně postupovat. Nechám tedy vždy na vás, kolik upřesňujících poznámek si budete (např. v rámci šetření času) vypisovat.

V podstatě nám pro uvažování nejdelšího úseku (KO, AO, OD, DC, PK) může bohatě stačit první z nákresů:

Ze všeho nejdřív bych doporučoval vypsat si z možností ty vzdálenosti, které jsou určeny přesně (pokud vůbec nějaké jsou). V našem případě je to vzdálenost úseku DC - tj. přesně 1/4 trati a úseku PK - tj. přesně 1/5 trati. Úsek PK můžeme rovnou eliminovat, jelikož 1/5 < 1/4. (Zbývají tedy úseky KO, AO, OD, DC).

Také je užitečné ihned eliminovat možnosti, které jsou jednoznačně kratší než jiné možnosti (jelikož jsou přímo jejich součástí). V našem případě je tedy úsek AO rozhodně kratší, než úsek KO, jelikož K je určitě nalevo od A. (Zbývají tedy úseky KO, OD, DC).

Mějte neustále na paměti, že máme-li vybrat např. nejdelší úsek - tento úsek opravdu musí být nejdelší za všech předpokladů. Tedy zejména v případě, kdy uvažujeme jeho nejkratší možnou délku a přitom u všech ostatních úseků uvažujeme jejich nejdelší možnou délku. (V případě hledání nejkratšího úseku budeme pochopitelně porovnávat jeho nejdelší délku s nejkratšími délkami ostatních úseků).

Také je důležité rozumět tomu, že například pro velikost úseku OD platí: 0<OD<1/4 (nikoliv 0≤OD≤1/4), protože bod O nemůže dosáhnout svých hraničních hodnot (věty v zadání byly totiž formulovány tak, že občerstvení je umístěno za polovinou cesty a že divadlo je až za občerstvením). Tím pádem i úsek OD můžeme eliminovat, jelikož OD je tedy kratší než úsek DC, který se svojí délkou 1/4 trati je zatím nejdelší známý úsek). (Zbývají tedy úseky KO, DC).

Zbývá nám určit délku posledního úseku: KO. Můžeme například využít toho, že jsme si dříve vzdálenosti vyjádřili ve zlomcích se společným jmenovatelem (tedy v šedesátinách) - pro délku úseku KO tedy platí: 18/60<KO (18/60 = 8/60+10/60), což je delší úsek než DC (1/4=15/60).