Jak na TSP - Analytické myšlení - Pravdy a lži
0% hotovo- Úvod
- Příklad 1
- Příklad 2
- Příklad 3
- Příklad 4
- Příklad 5
- Příklad 6
- Příklad 7
- Příklad 8
- Příklad 9
- Příklad 10
- Příklad 11
- Příklad 12
- Příklad 13
- Příklad 14
- Příklad 15
- Příklad 16
- Příklad 17
Sestavili jsme pro vás unikátní videokurz, který vám pomůže s vaší přípravou na přijímčky Masarykovy univerzity. Čekají na vás desítky hodin výukových videomateriálů a mnoho dalších užitečných podkladů. Nabyté znalosti si můžete prověřovat procházením kvízů. Pomocí statistik můžete sledovat, jak se v jednotlivých oblastech lepšíte, případně se můžete porovnávat s dalšími studenty. Svůj výsledek také můžete sdílet například na Facebooku a pochlubit se tak vašim přátelům.
Kurz nemáte koupený (nebo jen nejste přihlášen/a), máte tedy přístup pouze k omezené části kurzu.
Koupit kurzTeorie
1. Sestavit všechny možné kombinace pravdivostních hodnot jednotlivých tvrzení (výroků)
Velmi užitečné je rozdělit si danou situaci na všechny možné kombinace pravdivostních hodnot tvrzení. Není to pro nás nic nového, celkem je takových situací právě 2n (kde n je počet tvrzení). Obvykle je v zadání tento počet kombinací omezen díky formulacím typu: "alespoň jeden z výroků je pravdivý", apod.
Ukažme si na příkladu:
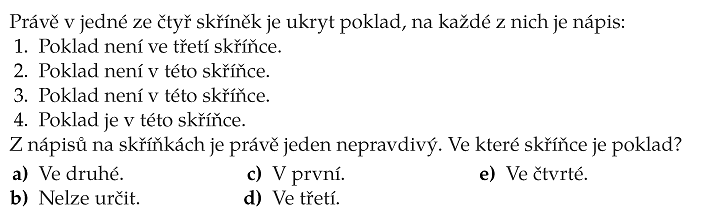
Zadání nás informuje o tom, že právě jeden z nápisů na skříňkách je nepravdivý, díky tomu si tedy situaci omezíme pouze na ty kombinace pravdivostních hodnot, kdy tři z tvrzení jsou pravdivé (1) a jedno nepravdivé (0). Je však třeba uvažovat všechny permutace - tj. nepravdivé tvrzení může z uvedených čtyř být postupně:
| pouze první | pouze druhé | pouze třetí | pouze čtvrté | |
|
1. (První skříňka) 2. (Druhá skříňka) 3. (Třetí skříňka) 4. (Čtvrtá skříňka) |
0 1 1 1 |
1 0 1 1 |
1 1 0 1 |
1 1 1 0 |
2. Zapsat jednotlivá tvrzení pomocí logických výrazů v jejich přímé a znegované podobě
Pro každé tvrzení vždy sepíšeme 2 logické výrazy - jeden z nich je přímým přepisem tvrzení (výroku), druhý z nich je jeho negací.
Pro náš případ tedy vypíšeme tyto logické výrazy (jednotlivé výrokové proměnné (P,D,T,Č) označují přítomnost pokladu v daných skříňkách (První, Druhé, Třetí, Čtvrté)) :
| výrok v přímé (nezměněné podobě) | výrok ve znegované podobě | |||||
|
1. (První skříňka) 2. (Druhá skříňka) 3. (Třetí skříňka) 4. (Čtvrtá skříňka) |
0 1 1 1 |
1 0 1 1 |
1 1 0 1 |
1 1 1 0 |
¬T ¬D ¬T Č |
T D T ¬Č |
Velmi důležité je si uvědomit, proč si vlastně vypisujeme výrok ve znegované podobě. Pokud například v první situaci máme pravdivostní hodnoty "0,1,1,1", znamená to, že u první skříňky budeme pracovat právě s touto znegovanou formou - tj. budeme předpokládat, že tento (znegovaný) výraz je pravdivý.
3. Procházet jednotlivé situace (kombinace pravdivostních hodnot) a hledat paradoxy
Nyní máme vše připravené pro to, abychom mohli určovat, kde se nachází poklad ve všech možných situacích (tj. všech kombinacích pravdivostních hodnot), a také budeme předpokládat, že při některých situacích vznikne paradox - tedy, že tuto situaci budeme moci eliminovat, jelikož pak není možné, aby taková situace nastala.
Můžeme postupovat dvěma základními postupy (oba vedou k cíli):
První způsob: Postupné procházení jednotlivých situací
Pozn. Následující postup budu popisovat velmi dopodrobna, aby měli všichni možnost jej správně pochopit. Bude se tedy možná jevit jako velmi zdlouhavý, ve skutečnosti však lze jednotlivé kroky automatizovat a po chvilce cviku jistě sami uznáte, že lze i tyto příklady řešit celkem svižně.
Procházíme tedy postupně jednotlivé situace a zjišťujeme, jak se vyvíjí (ohledně pozice pokladu). Budeme proto procházet postupně jednotlivé řádky a pracovat postupně s jednotlivými proměnnými:
- pokud jsme proměnnou ještě neohodnotili, tak ji ohodnotíme nyní (tak aby hodnota tvrzení byla pravdivá)
- pokud jsme proměnnou ohodnotili již dříve, tak ověříme, zdali po dosazení do tvrzení vyjde tvrzení pravdivé (v pořádku) nebo nepravdivé (paradox - jelikož chceme, aby všechna tvrzení byla pravdivá)
V našem případě tedy začneme u první situace, kdy uvažujeme, že nápisy na druhé, třetí i čtvrté skříňce jsou pravdivé a také že je pravdivá znegovaná forma nápisu na první skříňce. Pravdivé jsou tedy tyto výroky:
- T ... tedy: poklad je v T ... označíme tedy T=1 (jelikož poklad je právě v jediné skřínce, můžeme označit hodnoty i zbývajících proměnných - tedy P=0, D=0 a Č=0)
- ¬D ... tedy: poklad není v D ... tvrzení vyhovuje již dříve přiřazeným hodnotám
- ¬T ... tedy: poklad je v T ... vzniká paradox vzhledem k prvnímu (vzhledem k přiřazeným hodnotám do proměnných), další tvrzení této situace nemusíme procházet
- Č ... tedy: poklad je v Č ... opět vzniká paradox vzhledem k prvnímu řádku (vzhledem k přiřazeným hodnotám do proměnných)
Při průchodu jednotlivými řádky jsme tedy došli k paradoxu - tato možnost tedy nemůže nastat a můžeme ji eliminovat.
Následující dvě situace přeskočíme (postup bude stejný jako v předešlé situaci). Jen tedy prozradím, že při průchodu dojde opět k paradoxu a tyto možnosti také eliminujeme. Postupy, jak řešit tyto příklady jsou podrobně popsány ve výukových videích a proto je můžete využít jako primární zdroj výuky. Příkladů na procvičování je v této kapitole dost.
Postoupíme tedy až ke čtvrté situaci, kdy jsou pravdivé první, druhé a třetí tvrzení a také znegovaná forma čtvrtého tvrzení. Pravdivé jsou tedy tyto výroky:
- ¬T ... tedy: poklad není v T ... označíme tedy T=0
- ¬D ... tedy: poklad není v D ... označíme tedy D=0
- ¬T ... tedy: poklad není v T ... T již je označeno, avšak jeho hodnota vyhovuje pravdivosti tohoto tvrzení
- ¬Č ... tedy: poklad není v Č ... označíme tedy Č=0
Jelikož tato situace konstatuje, že ve skříňkách D, T ani Č se poklad nenachází, je jasné, že poklad se tedy musí nacházet ve skříňce P (zadání říká: právě v jedné ze čtyř skříněk je poklad).
Druhý způsob: Jak ušetřit nějaký čas
Umíme-li v příkladech tohoto typu dobře chodit. Můžeme jednotlivé možnosti eliminovat velmi rychle. Podíváme-li se například letmo na naši sestavenou tabulku, můžeme si jistých paradoxů všimnout okamžitě:
| výrok v přímé (nezměněné podobě) | výrok ve znegované podobě | |||||
|
1. (První skříňka) 2. (Druhá skříňka) 3. (Třetí skříňka) 4. (Čtvrtá skříňka) |
0 1 1 1 |
1 0 1 1 |
1 1 0 1 |
1 1 1 0 |
¬T ¬D ¬T Č |
T D T ¬Č |
Ze zadání je zřejmé, že poklad nemůže současně být ve více skřínkách, takže můžeme například eliminovat ty možnosti, které na první pohled tento fakt umožňují:
- nepravdivý nápis na první i druhé skřínce (neeliminuje žádnou možnost)
- nepravdivý nápis na druhé i třetí skřínce (neeliminuje žádnou možnost)
- pravdivý nápis na čtvrté skřínce a nepravdivý na první skřínce (eliminuje první možnost)
- pravdivý nápis na čtvrté skřínce a nepravdivý na první skřínce (eliminuje druhou možnost)
- pravdivý nápis na čtvrté skřínce a nepravdivý na první skřínce (eliminuje třetí možnost)
Je možné, že přehlédnete některé možnosti, které by se daly eliminovat (tvrzení v jiných příkladech bývají obvykle složitější). To však ničemu nevadí - všechny možnosti, které vám zůstanou budete následně procházet prvně zmíněným ("zdlouhavým") způsobem a nakonec opět zbudou pouze ty situace, které neobsahují paradox a se kterými je tedy pro určování správného výsledku počítat.
4. Na základě vyhovujících situací vyhodnotit správný výsledek
Jelikož jsme eliminovali 3 nabízející se situace, zbyla nám jediná - a to ta, při které se poklad nachází v první skřínce.
Procvičovací kvíz
Pravdy a lži
Informace o kurzu Jak na TSP
Veškerá zadání úloh TSP jsou duševním vlastnictvím Masarykovy univerzity a jsou užita na základě licence poskytnuté Masarykovou univerzitou. Veškeré vysvětlující komentáře a doprovodné texty k jednotlivým úlohám jsou produktem autora kurzu a Masarykova univerzita nezaručuje jejich správnost.
Masarykova univerzita nabízí uchazečům o studium zdarma stažení všech dosavadních variant TSP i s klíčem správných odpovědí, včetně e-learningového kurzu, na adrese http://muni.cz/tsp, kde mohou uchazeči o studium rovněž nalézt odkazy i na další služby poskytované Masarykovou univerzitou - Diskusní fórum pro uchazeče, Interaktivní online TSP, Často kladené dotazy, aj.



Diskuze
Reagovat na celek